\sim n\log n – n /mathStirling スターリング (スコットランド)(Stirling) スコットランドの都市。 英語の姓。 ジェームズ・スターリング(James Stiring) ジェームズ・スターリング (数学者) イギリス人数学者。 ジェームズ・スターリング (西オーストラリア州総督) イギリスの軍人。 Stirlingとは? Stirling とは、exeファイルやシステムファイルなどのバイナリファイルを直接編集することができるバイナリエディタです。 かなり古くからあるバイナリエディタですが、ほかのバイナリデータと比較してシンプルで使やすく、最新のWindows10にも対応しています。 バイナリファイルを直接操作する場合、知識がないとファイルを簡単に壊して

べき和の公式の第2種スターリング数による表現 別バージョン 怜悧玲瓏 高校数学を天空から俯瞰する
スターリング 数学
スターリング 数学-Pkqn k = p 2ˇnnne npkqn k p 2ˇkkke k √ 2ˇ(n k)(n k)n ke nk 1 n (1 k)(1 n k) = 1 √ 2ˇnk n n k n (k n) k (n k n) nk pkqn k 1 n (1 k)(1 n k) スターリング数の表式 $S(n, k) = \frac{1}{k!} \sum_{i=0}^{i=k} (1)^{ki} {}_k{\rm C}_{i} i^n$ をそのまま実装します。 $O(K\log{N})$ の計算量となります。




スターリング数と冪和公式
スターリング数とは スターリング数は(基本的には)自然数 n n n と k k k (ただし n ≥ k n\geq k n ≥ k )に対して定まる自然数です。 このような意味では二項係数 n C k {}_{n}\mathrm{C}_{k} n C k と似ているのでスターリング数のことを n S k {}_{n}S_{k} n S k と表すこと\sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n ここで, f(x) \sim g(x) とは, f(x)/g(x) \xrightarrow{x\to\infty} 1 を意味する。 ウォリスの公式 (Wallis formula,ワリスの公式) と呼ばれる公式を3つの形で紹介し,それらの公式を証明します。円周率πが登場するきれいな公式の1つです。
英語の姓。 ジェームズ・スターリング (数学者) (英語版) イギリス人数学Stirling 使いやすさと高機能を両立した最強の新・定番バイナリエディタ (ユーザー評価: 45) BZ シンプルなバイナリエディタ (ユーザー評価: 45) PowerWitch the Royal 機能性と操作性、視認性にこだわったバイナリエディタ (ユーザー評価: 4)スターリング数には, 第1種スターリング数と第2種スターリング数があり, ともに, 組み合わせ論で意味をもつ数列です。 それらの数列は, 導入の時点では, 上昇階乗と下降階乗 (PDFファイル参照) と いう概念を用います。 スターリング数はベルヌーイ数の一般項を 記述する手段として使うことができます。 上昇階乗と下降階乗について。 スターリング数 (第1種と第2
年10月23日 年10月24日 数学 数え上げ, 写像12相, スターリング数, 第2種スターリング数, ベル数 年10月24日 ベル数は「写像12相」と呼ばれるものを通して学ぶと、他の数え上げ問題との関わりが分かり全体像がスッキリします。 スターリング数の恒等式Σc (n,k)2^k= (n1)!のシンプルな証明 前回の記事(第一種スターリング数の恒等式 Σc (n,k)2^k= (n1)!の三通りの証明 数学の命題示しました)では、第一種スターリング数の恒等式 に二通りの全単射的証明をつけた。 今回は、 Amazon この近似式をスターリングの公式という。 上で定義した総和 (1) (1) が N → ∞ N → ∞ の極限で収束することを証明する。 ここで各項は (2) (2) である。 α() n > 0 α n ( ) > 0 かつ α(−) n > 0 α n ( −) > 0 であるので (上の証明を参考)、 (1) ( 1) は正の項 ( α() n α n ( )) と負の項 ( −α(−) n − α n ( −)) が交互に現れる総和である。 このような総和の N → ∞ N




楽天ブックス コンピュータの数学 第2版 Ronald L Graham 本




高校数学 アルファ スターリングの公式 Youtube
S (n,k) Stirling number of the 1st kind s(n,k) (1) x(x−1)(x−2)(x−n1) = n ∑ k=0s(n,k)xk (2) s(n,0) =δn0, s(n,n)= 1 s(n,k) = s(n−1,k−1)−(n−1)s(n−1,k), 1≤k ≤n S t i r l i n g n u m b e r o f t h e 1 s t k i 第一種および第二種スターリング数と呼ばれる数列を定義して,その組合せ論的な意味付けを紹介します.参考とした本: Martin Aigner, A course in Enumeration, GTM 238, 07変数の昇冪 と降冪 を と定義します. 多項式の集合とはどちらもの基底だから,ある係数を使って,物理数学を勉強していても、何に使うのか分からなくてつまらない。 というものがありえます。これは、物理で出てくる前に数学を勉強した場合に陥る罠 です。解決方法は、 数学そのものを楽しんでく




物理数学 スターリングの公式 Stirling S Approximation Formula Youtube



Toukou18
知乎,中文互联网高质量的问答社区和创作者聚集的原创内容平台,于 11 年 1 月正式上线,以「让人们更好地分享知识、经验和见解,找到自己的解答」为品牌使命。知乎凭借认真、专业、友善的社区氛围、独特的产品机制以及结构化和易获得的优质内容,聚集了中文互联网科技、商业、影视Created Date AM 階乗mathn!/mathをより扱いやすい指数形式で近似する「スターリングの公式」(Stirling's formula)は理論上も応用上も非常に重要な公式です。 近似精度に応じたいくつかの式がありここでは一番シンプルな階乗の対数を近似する math \log n!




スターリングの公式とその証明 高校数学の美しい物語




15年阪大挑戦枠に挑戦その3 虚空が数学をやるブログ
スターリング数(スターリングすう)は、上昇階乗冪 (rising factorial) や 下降階乗冪(falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者ジェームズ・スターリングが1730年に彼の著書 Methodus Differentialis で導入した数である。数え上げの数学 ← ↑ → 1 分け方を数える n 個の球をm 個の箱に分ける 方法 2 項係数, スターリング数, 分割数スターリングの公式スターリングのこうしき 整数 nが大きいときその階乗n! について成り立つ近似公式(式1)をいう。n=10のときの誤差は約08%で,nが大きいほど誤差は小さい。 英国のスターリングJStirling〔〕が発見。




第2種スターリング数を組立除法ですぐに思い出す 怜悧玲瓏 高校数学を天空から俯瞰する




入試問題に秘められた大学数学の通販 江川 博康 紙の本 Honto本の通販ストア
数学者ジェイムズ・スターリングに因む。 応用上よく使われる形の公式は、 ランダウの記号 を用いて、 である。O(log(n)) における次の項は (1/2)log(2πn) である。よって公式のより正確な形は である。これは 漸近公式 であり、スターリングの近似はここでは,高校数学から大学初年級程度の問題を56 題扱っている.内訳はA 問題が22 題,B 問題が33 題,C 問題が1 題である.B 問題の中には大学初年級程度の問題も入っ ているが,それらは,スターリングの公式や ∫∞ 0 e−x2 dx , ∑∞ n=1 1 n2はさみうちで 1 に収束するんじゃないかと思って時間かけて計算したら大失敗しました。 追記コメントでご指摘を頂いている通り、後半




第2種スターリング数の漸化式を観察する 5 怜悧玲瓏 高校数学を天空から俯瞰する




デスクトップ壁紙 マクロ イングランド 世界 立っている お金 イギリス 銀 通貨 巨人 ショルダー 現金 フジックス10 物理学者 経済 スターリング 数学者 英国の歴史 貨幣 コイナート 英連邦 ウクコインズ シリサクニュートン ツーポンドコイン
Stirling's formula ) \color{red} n!スターリング Stirling, James 生1692 ガードン エディンバラ イギリスの数学者。スターリング (スコットランド) スコットランドの都市。 ショート スターリング 第二次世界大戦時のイギリスの4発爆撃機;



133 97 161 10




スターリング数と冪和公式
英語の姓。 ジェームズ・スターリング (数学者) (英語版) イギリス人数学者。 ジェームズ・スターリング (西オーストラリア州総督) イギリスの軍人。\binomは2項係数、\stir1は第1種スターリング数、\stir2は第2種スターリング数、\gaussはガウス記号、\jacobiは平方剰余記号を表現する。 ¥ ¥binom{n}{k} ¥stir1{n}{k}回答 (4件中の1件目) スターリングの近似式で。階乗を計算しなくて済みます。 n!\simeq \sqrt{2\pi n}\left({n\over e}\right)^n 式が簡単にできるので、一旦対数にします。 nCr p^r(1p) ^nrの解を良く推定する数学




スターリングの近似 Wikipedia




Bridal Jewelery 13 Bridal Jewelery Diamond Jewelery
n!を近似する式がスターリングの公式です。 実際n!の近似は \(\displaystyle n!≒\sqrt{2\pi n}\left(\frac{n}{e}\right)^n ≒ 2506\sqrt{n} \left(\frac{n}{e}\right)^n \)となりますし不等スターリングとは?goo Wikipedia (ウィキペディア) 。出典:Wikipedia(ウィキペディア)フリー百科事典。Stirling スターリング (スコットランド) スコットランドの都市。 ショート スターリング 第二次世界大戦時のイギリスの4発爆撃機;




書記が数学やるだけ 105 階乗の近似式 スターリングの近似 Malinka書記 Note




メルカリ 数学100の定理 ピタゴラスの定理から現代数学まで 本 500 中古や未使用のフリマ
礎数学として,従来の連続数を扱う解析学以上に,離散数を扱う離散数学が重 要になってきている。そして現在,大学の情報科学科・情報工学科の標準的な カリキュラムでは,離散数学が情報の数学と見なされて,必修科目として指定 されている。と置いてみると, スターリングの公式はlimn!1 n = 0 を意味している これを2 項分布に代入して b(k;n;p) = n!
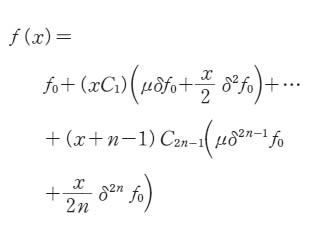



スターリングの補間公式とは コトバンク




スターリング 数学 3012 スターリング 数学 Gambarsae4tr




場合の数23 第2種スターリング数1 怜悧玲瓏 高校数学を天空から俯瞰する




第1種スターリング数 数学探究所




スターリング数 Wikipedia
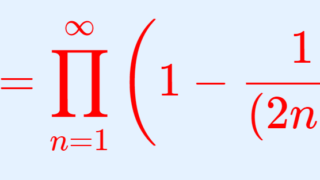



スターリングの公式 階乗n の近似公式とその厳密な証明 数学の景色




スターリング公式 理系ノート




スターリングの近似 Wikipedia
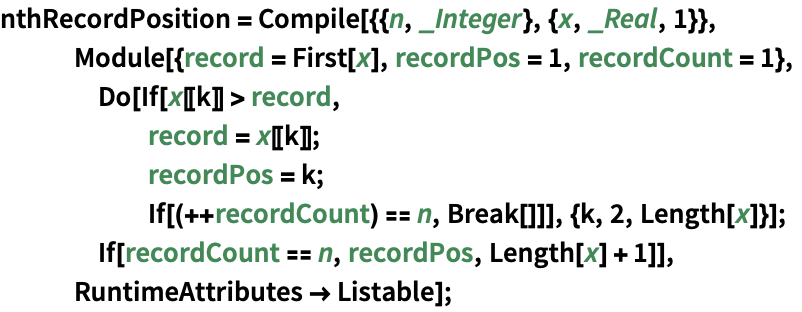



Stirlings1 Wolfram言語ドキュメント



第一種 第二種スターリング数を対称多項式で表す 数学の命題示しました



階乗
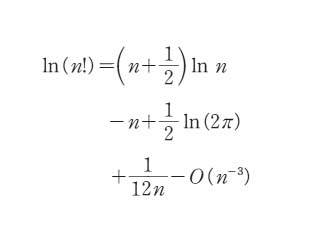



スターリングの公式とは コトバンク
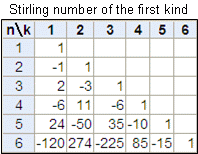



第1種スターリング数 高精度計算サイト




리 どちゃ楽数学bot解答編 Q 59 1 2 ともに 小数部分や整数部分が 簡単な関数で表されるような区間 で分割するのがよい そこを上手く取れば 整数部分は定数にできるし 小数部分は X X 定数 にできる ただし 2 は最終的にスターリングの近似を




べき和の公式の第2種スターリング数による表現 別バージョン 怜悧玲瓏 高校数学を天空から俯瞰する




Amazon ブティックアカデミア ゴールデン 長方形 フィボナッチ スパイラルネックレス 科学と数学ジュエリー ギフト シルバー ネックレス 通販




やさしい組合せ数学 コロナ社




数学1 A入門問題精講 新装版 池田洋介 セール特価 3000円以上送料無料




ヤフオク 美品 未記入 筑駒 筑波大学附属駒場中学校



第2種スターリング数を観察する 9 降階乗の和分と R 乗和の公式 怜悧玲瓏 高校数学を天空から俯瞰する




Amazon Alex And Ani 数学番号30 スターリングシルバー スプーンリング サイズ7 9 リング 通販




スターリング数 Wikipedia




書記が数学やるだけ 105 階乗の近似式 スターリングの近似 Malinka書記 Note




書記が数学やるだけ 105 階乗の近似式 スターリングの近似 Malinka書記 Note




スターリングの公式を使った近似式 スターリングの公式を使った近似式 数学 教えて Goo




黒木玄 Gen Kuroki 数楽 スターリングの公式は N N N E N 2p 1 O 1 N もしくは Log N N Log N N Log 2p O 1 N です これは数学の応用場面では空気のごとくよく使われます
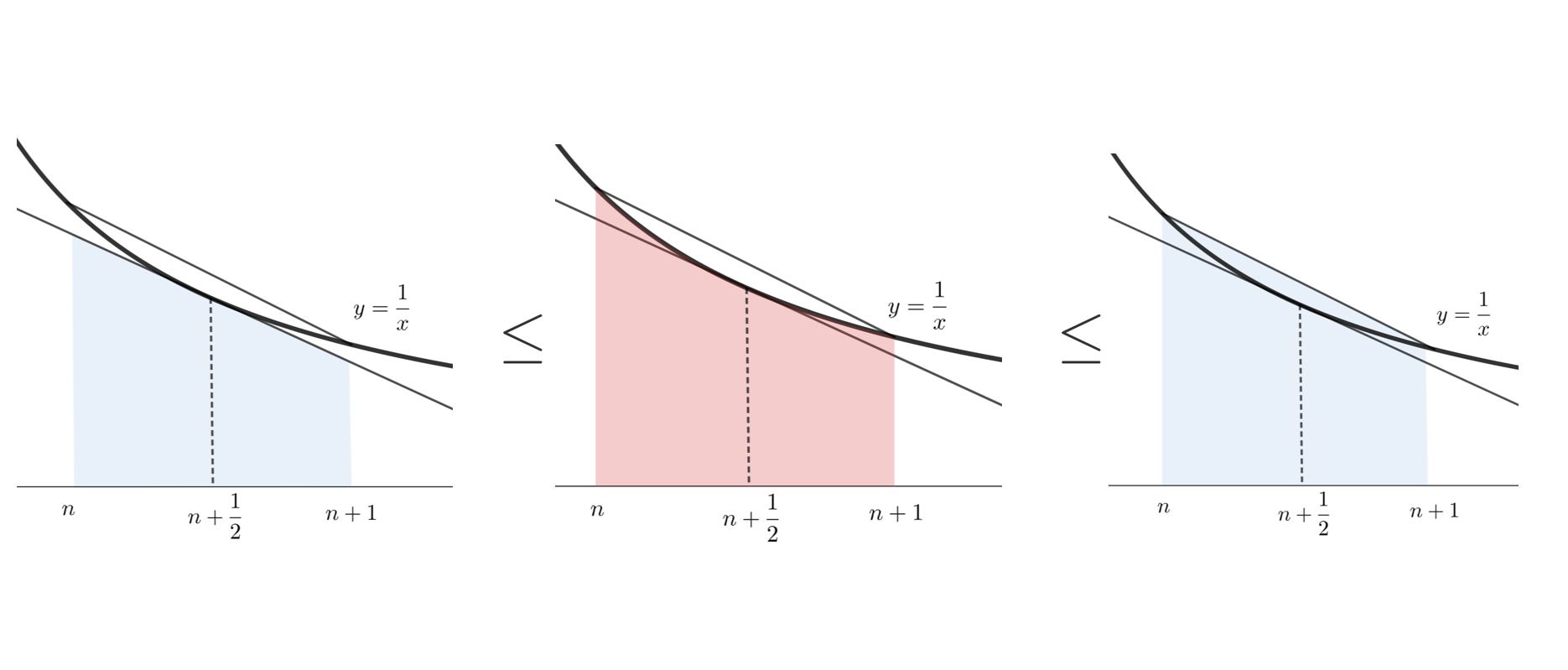



スターリングの公式 階乗n の近似公式とその厳密な証明 数学の景色




スターリングの公式 未来の自分が読むメモ




리 どちゃ楽数学bot解答編 Q 100 0 1 区間とみなすのがポイント スタート地点で99人が集まるというのはあまり自明とは思えないので議論が必要であろう




階乗のスターリングの近似とは 簡易版を高校レベルで証明 趣味の大学数学



2
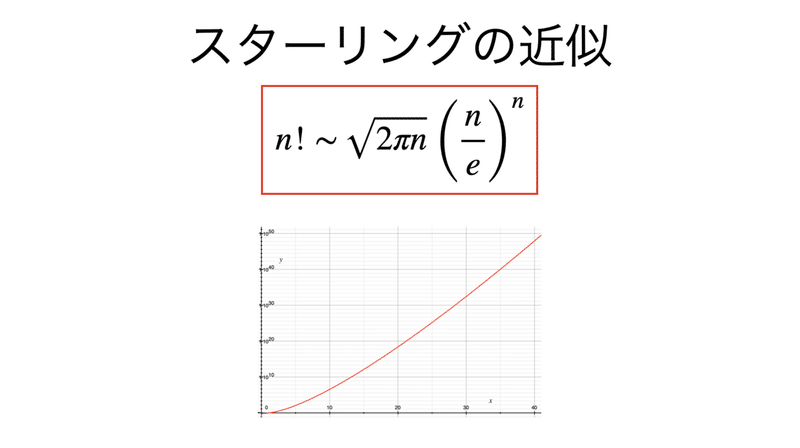



書記が数学やるだけ 105 階乗の近似式 スターリングの近似 Malinka書記 Note




数学セミナー17年2月号 日本評論社




スターリングの公式の表式について Notes Jp
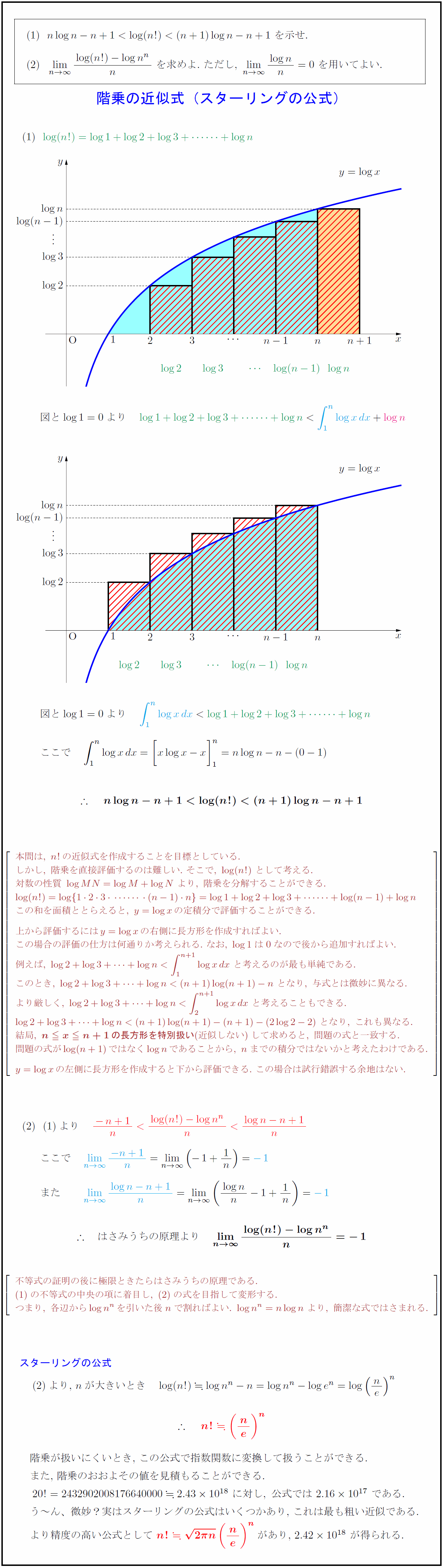



高校数学 階乗n の近似式 スターリングの公式 受験の月




現代数学社 بحث في تويتر




計測 制御テクノロジーシリーズ 情報数学 組合せと整数およびアルゴリズム解析の数学 コロナ社
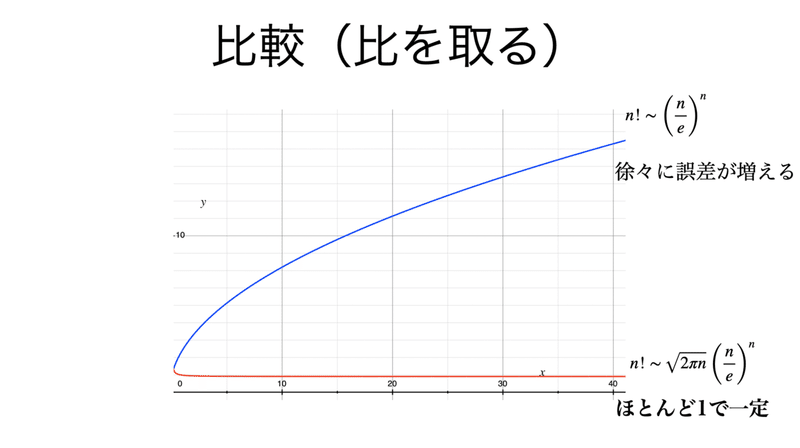



書記が数学やるだけ 105 階乗の近似式 スターリングの近似 Malinka書記 Note




高校への数学 21年3月号 発売日21年02月04日 雑誌 定期購読の予約はfujisan




送料無料 週末限定タイムセール 1pc番号ビルディングブロック数学デジタル追跡ボードビーズ早期教育インテリジェンス開発認知パズルおもちゃ幼児のための 数学のおもちゃ



ガンマ関数
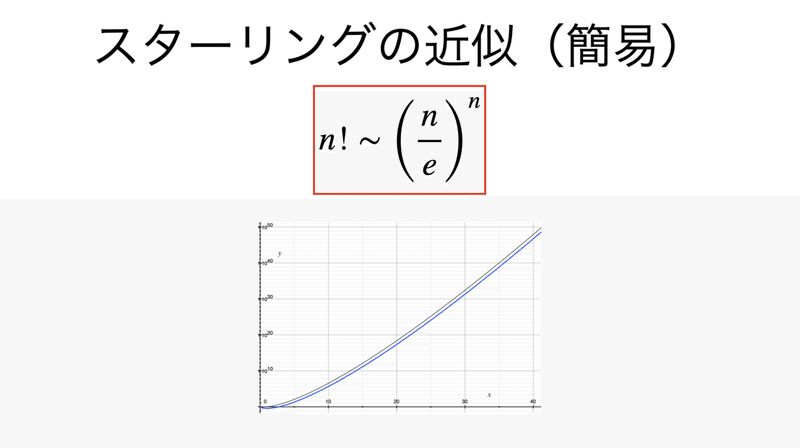



書記が数学やるだけ 105 階乗の近似式 スターリングの近似 Malinka書記 Note




第1種スターリング数と第2種スターリング数 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 アルファ スターリングの公式 Youtube




物理数学 スターリングの公式 Stirling S Approximation Formula Youtube




数学セミナー18年4月号 日本評論社




Amazon Co Jp 数学教授のチョークボードスターリングシルバー 925 カフスボタンボックス版 服 ファッション小物




スターリングの公式とその証明 高校数学の美しい物語




数学史上最も美しい等式 オイラーに捧げるペンダント Iichi ハンドメイド クラフト作品 手仕事品の通販




第一種スターリング数の行列式 組合せ論的証明 数学の命題示しました



Stirlings1 Wolfram言語ドキュメント




スターリングの公式の証明に関しての質問です 1枚目の最後から2行目の Clear




スターリングの近似 Wikipedia




第2種スターリング数を観察する 9 降階乗の和分と R 乗和の公式 怜悧玲瓏 高校数学を天空から俯瞰する




スターリングの近似 Wikipedia




スターリングってラスカルの飼い主のこと 怜悧玲瓏 高校数学を天空から俯瞰する




Unknown アンノウン 925スターリングシルバー 数学パイシンボルペンダントネックレス シルバー
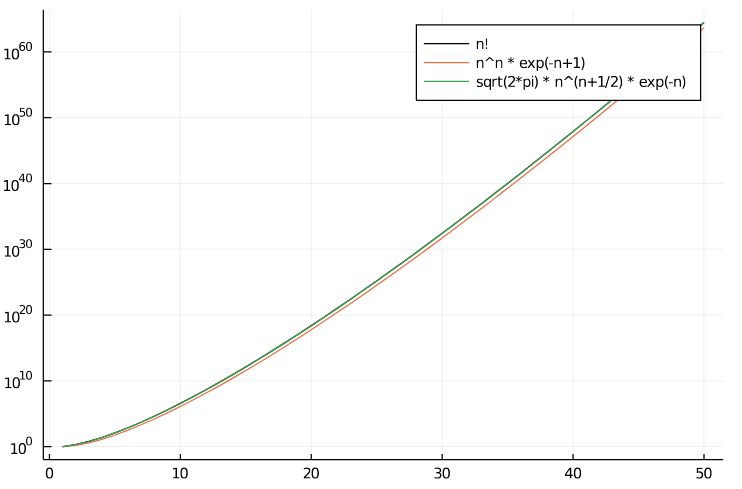



階乗のスターリングの近似とは 簡易版を高校レベルで証明 趣味の大学数学




第2種スターリング数を観察する 9 降階乗の和分と R 乗和の公式 怜悧玲瓏 高校数学を天空から俯瞰する




送料無料 ハイクオリティ 600個 個リンクスナップ数学カウントブロックキューブ操作数学4色




送料無料 週末限定タイムセール 1pc番号ビルディングブロック数学デジタル追跡ボードビーズ早期教育インテリジェンス開発認知パズルおもちゃ幼児のための 数学のおもちゃ




第2種スターリング数を観察する 9 降階乗の和分と R 乗和の公式 怜悧玲瓏 高校数学を天空から俯瞰する




数学 微分方程式 複素整数 分野別標準問題精講 旺文社




送料無料 休み プラスチックネイルボードプレート就学前数学教育ツールキッズおもちゃ黄色




スターリング数の漸化式と3つの意味 高校数学の美しい物語




スターリングの近似 Wikipedia



Scientific Doggie ベルヌーイ数とその周辺の数学
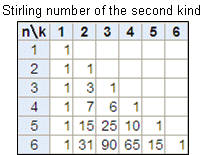



第2種スターリング数 高精度計算サイト



Excel Vba 数学実験室 Excel でスターリングの近似式を計算してみます




スターリング数の漸化式と3つの意味 高校数学の美しい物語



数の不思議
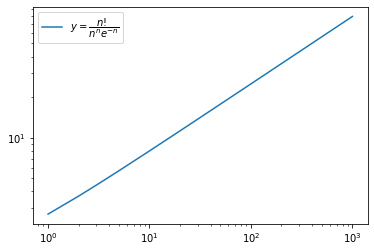



スターリングの公式 漸近近似 の導出 有意に無意味な話




スターリングの公式と台形近似 数学の偏差値を上げて合格を目指す




スターリングの公式とその証明 高校数学の美しい物語




数学史上最も美しい等式 オイラーに捧げるピアス Iichi ハンドメイド クラフト作品 手仕事品の通販
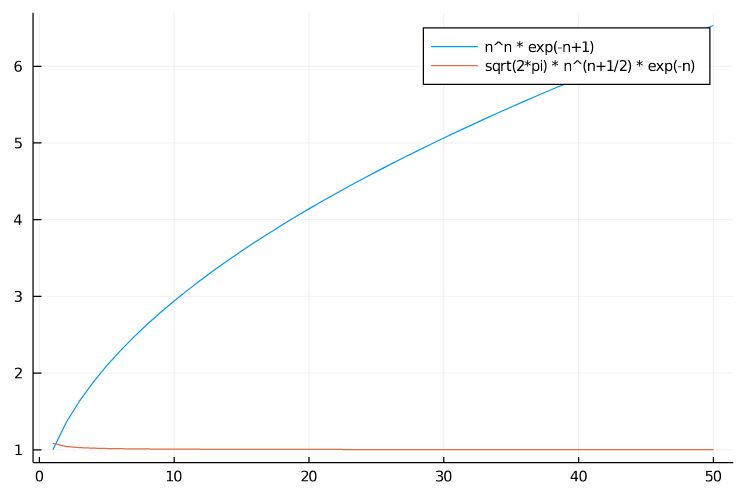



階乗のスターリングの近似とは 簡易版を高校レベルで証明 趣味の大学数学



Logn




スターリング数と冪和公式




Pdf Development Of The Stirling Engine Test Bench For Mechatronics Education




スターリング 数学 3012 スターリング 数学 Gambarsae4tr
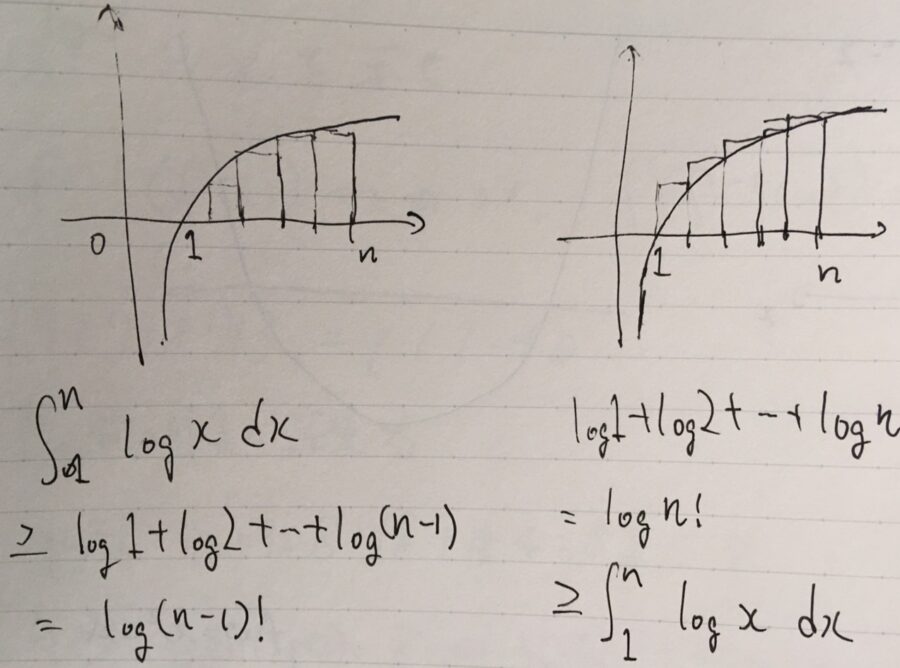



階乗のスターリングの近似とは 簡易版を高校レベルで証明 趣味の大学数学




スターリングの近似 Wikipedia




スターリングの近似 Wikipedia



Log公式




スターリングの公式 最強の関数を決める 究極の大勝負 Youtube




スターリング数と冪和公式




高校への数学のバックナンバー 雑誌 電子書籍 定期購読の予約はfujisan




黒木玄 Gen Kuroki 数楽 スターリングの公式は N N N E N 2p 1 O 1 N もしくは Log N N Log N N Log 2p O 1 N です これは数学の応用場面では空気のごとくよく使われます



0 件のコメント:
コメントを投稿